4 Data understanding
In data understanding, you:
- Import data
- Clean data
- Format data properly
- Create new variables
- Get an overview about the complete data
- Split data into training and test set using stratified sampling
- Discover and visualize the data to gain insights
4.2 Clean data
To get a first impression of the data we take a look at the top 4 rows:
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity |
|---|---|---|---|---|---|---|---|---|---|
| -122 | 38 | 41.0years | 880 | 129 | 322 | 126 | 8.3 | 452600.0$ | NEAR BAY |
| -122 | 38 | 21.0 | 7099 | 1106 | 2401 | 1138 | 8.3 | 358500.0 | NEAR BAY |
| -122 | 38 | 52.0 | 1467 | 190 | 496 | 177 | 7.3 | 352100.0 | NEAR BAY |
| -122 | 38 | 52.0 | 1274 | 235 | 558 | 219 | 5.6 | 341300.0 | NEAR BAY |
Notice the values in the first row of the variables housing_median_age and median_house_value. We need to remove the strings “years” and “$” with the function str_remove_all from the stringr package. Since there could be multiple wrong entries of the same type, we apply our corrections to all of the rows of the corresponding variable:
library(stringr)
housing_df <-
housing_df %>%
mutate(
housing_median_age = str_remove_all(housing_median_age, "[years]"),
median_house_value = str_remove_all(median_house_value, "[$]")
)We don’t cover the phase of data cleaning in detail in this tutorial. However, in a real data science project data cleaning is usually a very time consuming process.
4.3 Format data
Next, we take a look at the data structure and check wether all data formats are correct:
Numeric variables should be formatted as integers (
int) or double precision floating point numbers (dbl).Categorical (nominal and ordinal) variables should usually be formatted as factors (
fct) and not characters (chr). Especially, if they don’t have many levels.
glimpse(housing_df)#> Rows: 20,640
#> Columns: 10
#> $ longitude <dbl> -122, -122, -122, -122, -122, -122, -122, -122, -1…
#> $ latitude <dbl> 38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38…
#> $ housing_median_age <chr> "41.0", "21.0", "52.0", "52.0", "52.0", "52.0", "5…
#> $ total_rooms <dbl> 880, 7099, 1467, 1274, 1627, 919, 2535, 3104, 2555…
#> $ total_bedrooms <dbl> 129, 1106, 190, 235, 280, 213, 489, 687, 665, 707,…
#> $ population <dbl> 322, 2401, 496, 558, 565, 413, 1094, 1157, 1206, 1…
#> $ households <dbl> 126, 1138, 177, 219, 259, 193, 514, 647, 595, 714,…
#> $ median_income <dbl> 8.3, 8.3, 7.3, 5.6, 3.8, 4.0, 3.7, 3.1, 2.1, 3.7, …
#> $ median_house_value <chr> "452600.0", "358500.0", "352100.0", "341300.0", "3…
#> $ ocean_proximity <chr> "NEAR BAY", "NEAR BAY", "NEAR BAY", "NEAR BAY", "N…The package visdat helps us to explore the data class structure visually:
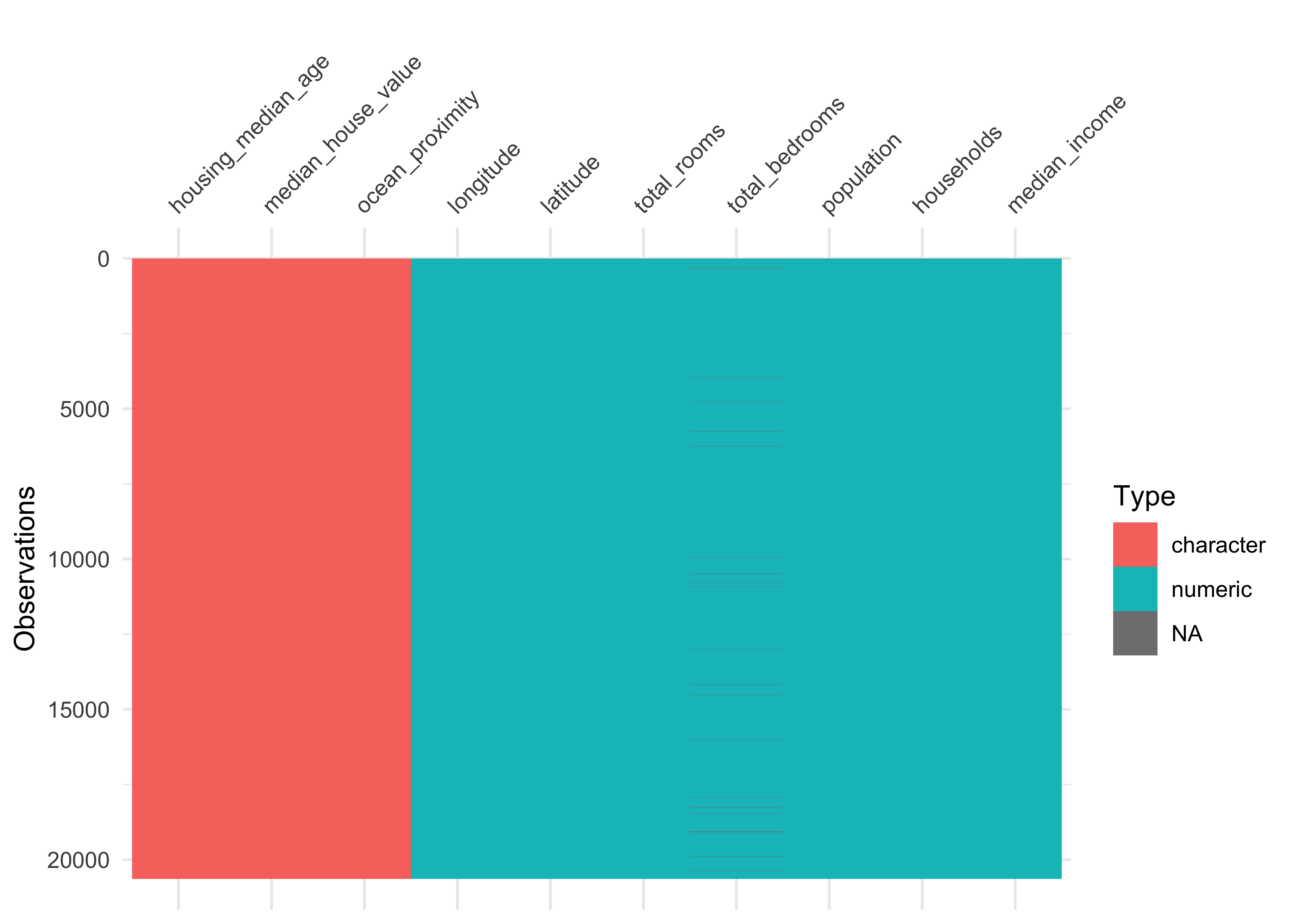
Figure 4.1: Overview about data classes
We can observe that the numeric variables housing_media_age and median_house_value are declared as characters (chr) instead of numeric. We choose to format the variables as dbl, since the values could be floating-point numbers.
Furthermore, the categorical variable ocean_proximity is formatted as character instead of factor. Let’s take a look at the levels of the variable:
housing_df %>%
count(ocean_proximity,
sort = TRUE)#> # A tibble: 5 x 2
#> ocean_proximity n
#> <chr> <int>
#> 1 <1H OCEAN 9136
#> 2 INLAND 6551
#> 3 NEAR OCEAN 2658
#> 4 NEAR BAY 2290
#> 5 ISLAND 5The variable has only 5 levels and therefore should be formatted as a factor.
Note that it is usually a good idea to first take care of the numerical variables. Afterwards, we can easily convert all remaining character variables to factors using the function across from the dplyr package (which is part of the tidyverse).
# convert to numeric
housing_df <-
housing_df %>%
mutate(
housing_median_age = as.numeric(housing_median_age),
median_house_value = as.numeric(median_house_value)
)
# convert all remaining character variables to factors
housing_df <-
housing_df %>%
mutate(across(where(is.character), as.factor))4.4 Missing data
Now let’s turn our attention to missing data. Missing data can be viewed with the function vis_miss from the package visdat. We arrange the data by columns with most missingness:
vis_miss(housing_df, sort_miss = TRUE)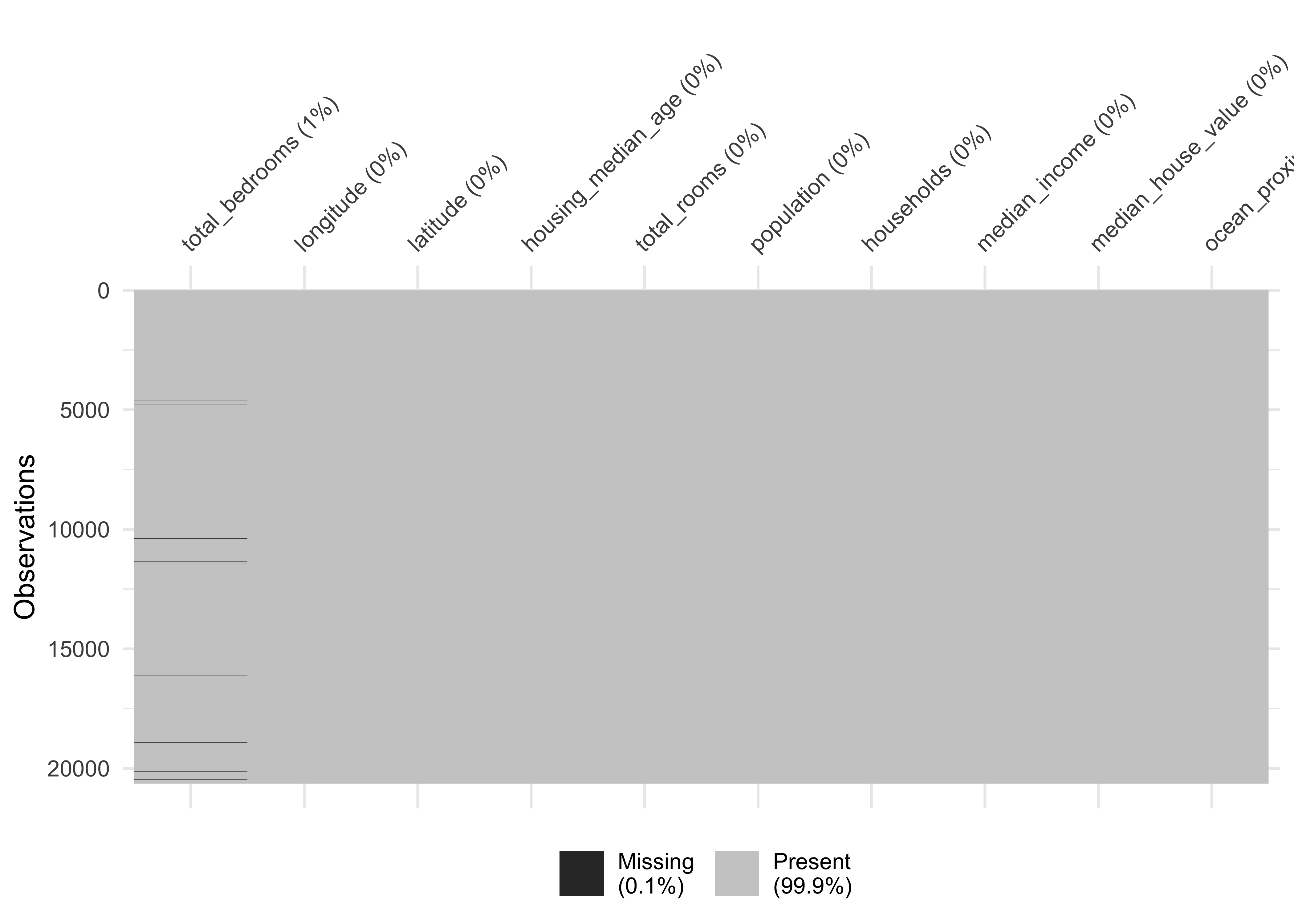
Figure 4.2: Overview about missing data
Here an alternative method to obtain missing data:
#> longitude latitude housing_median_age total_rooms
#> 0 0 0 0
#> total_bedrooms population households median_income
#> 207 0 0 0
#> median_house_value ocean_proximity
#> 0 0We have a missing rate of 0.1% (207 cases) in our variable total_bedroms. This can cause problems for some algorithms. We will take care of this issue during our data preparation phase.
4.5 Create new variables
One very important thing you may want to do at the beginning of your data science project is to create new variable combinations. For example:
the total number of rooms in a district is not very useful if you don’t know how many households there are. What you really want is the number of rooms per household.
Similarly, the total number of bedrooms by itself is not very useful: you probably want to compare it to the number of rooms.
And the population per household also seems like an interesting attribute combination to look at.
Let’s create these new attributes:
housing_df <-
housing_df %>%
mutate(rooms_per_household = total_rooms/households,
bedrooms_per_room = total_bedrooms/total_rooms,
population_per_household = population/households)4.6 Data overview
After we took care of our data problems, we can obtain a data summary of all numerical and categorical attributes using a function from the package skimr:
skim(housing_df)| Name | housing_df |
| Number of rows | 20640 |
| Number of columns | 13 |
| _______________________ | |
| Column type frequency: | |
| factor | 1 |
| numeric | 12 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| ocean_proximity | 0 | 1 | FALSE | 5 | <1H: 9136, INL: 6551, NEA: 2658, NEA: 2290 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| longitude | 0 | 1.00 | -1.2e+02 | 2.0e+00 | -124.35 | -1.2e+02 | -118.5 | -1.2e+02 | -114 | ▂▆▃▇▁ |
| latitude | 0 | 1.00 | 3.6e+01 | 2.1e+00 | 32.54 | 3.4e+01 | 34.3 | 3.8e+01 | 42 | ▇▁▅▂▁ |
| housing_median_age | 0 | 1.00 | 2.9e+01 | 1.3e+01 | 1.00 | 1.8e+01 | 29.0 | 3.7e+01 | 52 | ▃▇▇▇▅ |
| total_rooms | 0 | 1.00 | 2.6e+03 | 2.2e+03 | 2.00 | 1.4e+03 | 2127.0 | 3.1e+03 | 39320 | ▇▁▁▁▁ |
| total_bedrooms | 207 | 0.99 | 5.4e+02 | 4.2e+02 | 1.00 | 3.0e+02 | 435.0 | 6.5e+02 | 6445 | ▇▁▁▁▁ |
| population | 0 | 1.00 | 1.4e+03 | 1.1e+03 | 3.00 | 7.9e+02 | 1166.0 | 1.7e+03 | 35682 | ▇▁▁▁▁ |
| households | 0 | 1.00 | 5.0e+02 | 3.8e+02 | 1.00 | 2.8e+02 | 409.0 | 6.0e+02 | 6082 | ▇▁▁▁▁ |
| median_income | 0 | 1.00 | 3.9e+00 | 1.9e+00 | 0.50 | 2.6e+00 | 3.5 | 4.7e+00 | 15 | ▇▇▁▁▁ |
| median_house_value | 0 | 1.00 | 2.1e+05 | 1.2e+05 | 14999.00 | 1.2e+05 | 179700.0 | 2.6e+05 | 500001 | ▅▇▅▂▂ |
| rooms_per_household | 0 | 1.00 | 5.4e+00 | 2.5e+00 | 0.85 | 4.4e+00 | 5.2 | 6.0e+00 | 142 | ▇▁▁▁▁ |
| bedrooms_per_room | 207 | 0.99 | 2.1e-01 | 6.0e-02 | 0.10 | 1.8e-01 | 0.2 | 2.4e-01 | 1 | ▇▁▁▁▁ |
| population_per_household | 0 | 1.00 | 3.1e+00 | 1.0e+01 | 0.69 | 2.4e+00 | 2.8 | 3.3e+00 | 1243 | ▇▁▁▁▁ |
We have 20640 observations and 13 columns in our data.
The
sdcolumn shows the standard deviation, which measures how dispersed the values are.The p0, p25, p50, p75 and p100 columns show the corresponding percentiles: a percentile indicates the value below which a given percentage of observations in a group of observations fall. For example, 25% of the districts have a
housing_median_agelower than 18, while 50% are lower than 29 and 75% are lower than 37. These are often called the 25th percentile (or first quartile), the median, and the 75th percentile.Further note that the median income attribute does not look like it is expressed in US dollars (USD). Actually the data has been scaled and capped at 15 (actually, 15.0001) for higher median incomes, and at 0.5 (actually, 0.4999) for lower median incomes. The numbers represent roughly tens of thousands of dollars (e.g., 3 actually means about $30,000).
Another quick way to get an overview of the type of data you are dealing with is to plot a histogram for each numerical attribute. A histogram shows the number of instances (on the vertical axis) that have a given value range (on the horizontal axis). You can either plot this one attribute at a time, or you can use ggscatmat from the package GGally on the whole dataset (as shown in the following code example), and it will plot a histogram for each numerical attribute as well as correlation coefficients (Pearson is the default). We just select the most promising variabels for our plot:
library(GGally)
housing_df %>%
select(
median_house_value, housing_median_age,
median_income, bedrooms_per_room, rooms_per_household,
population_per_household) %>%
ggscatmat(alpha = 0.2)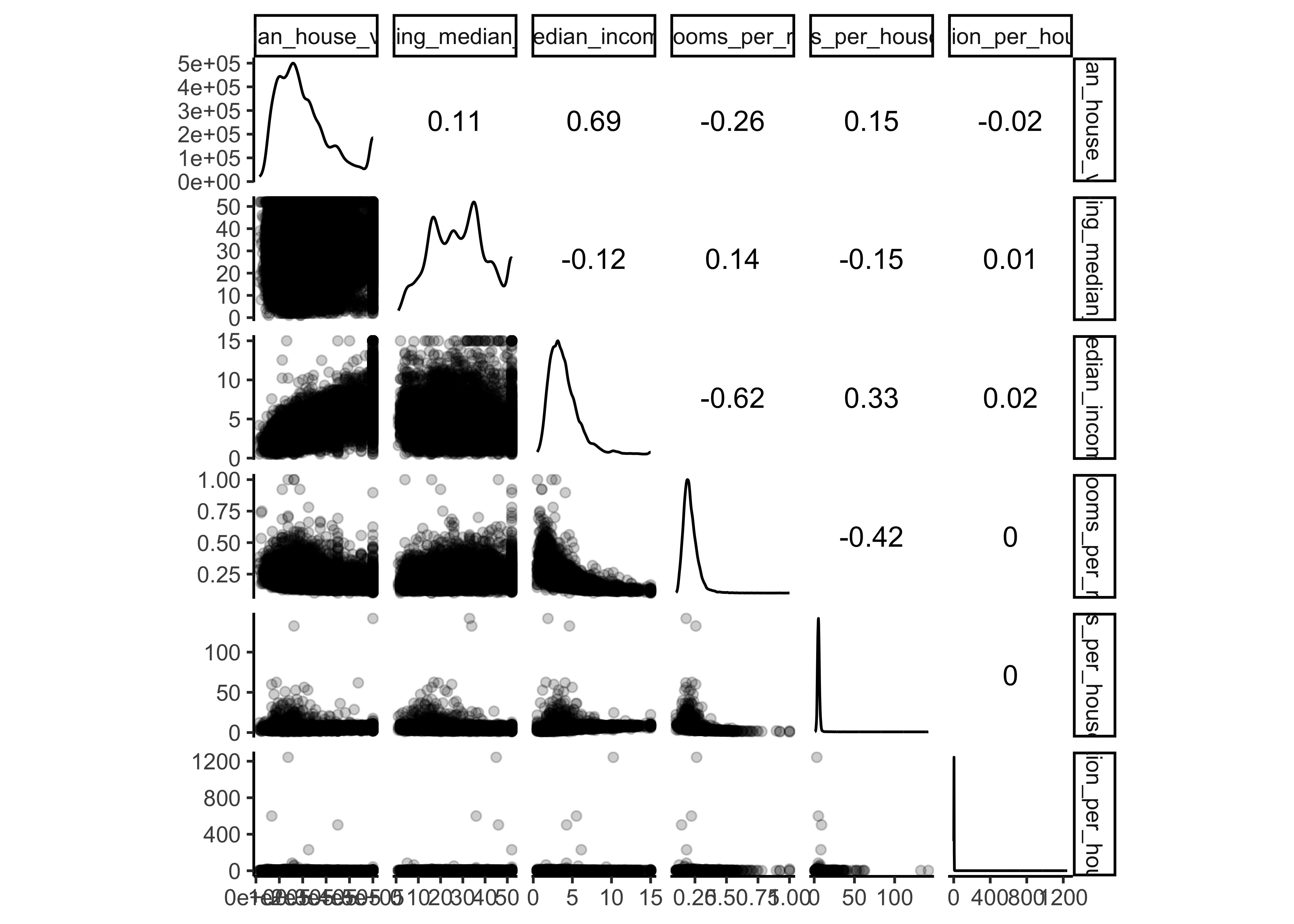
Another option is to use ggpairs, where we even can integrate our categorical variable ocean_proximity in the output:
library(GGally)
housing_df %>%
select(
median_house_value, housing_median_age,
median_income, bedrooms_per_room, rooms_per_household,
population_per_household,
ocean_proximity) %>%
ggpairs()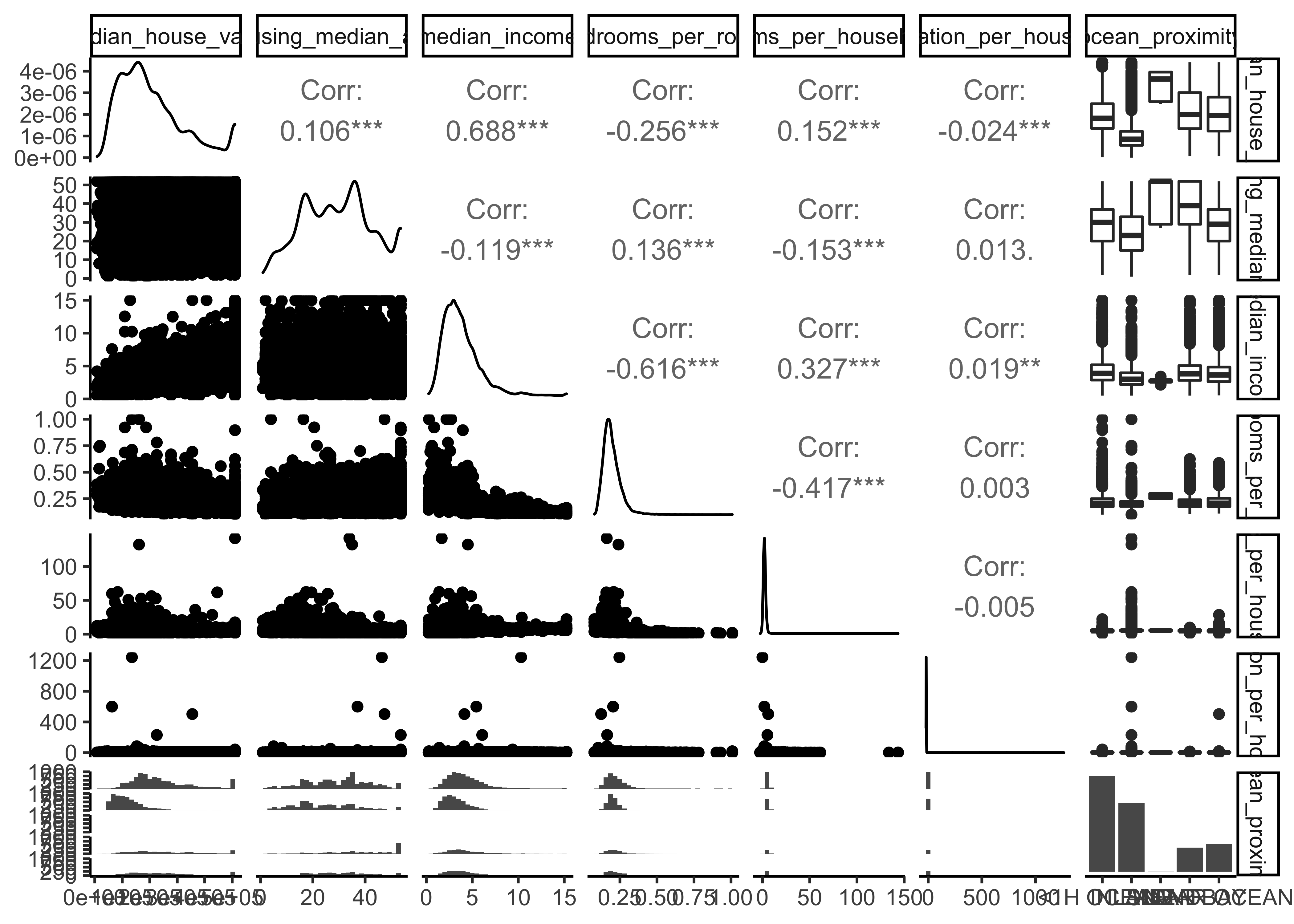
There are a few things you might notice in these histograms:
The variables median income, housing median age and the median house value were capped. The latter may be a serious problem since it is our target attribute (your y label). Our Machine Learning algorithms may learn that prices never go beyond that limit. This will be a serious problem if we need predictions beyond 500,000. We take care of this issue in our data preparation phase and only use districts below 500,000.
Note that our attributes have very different scales. We will take care of this issue later in data preparation, when we use feature scaling (data normalization).
Finally, many histograms are tail-heavy: they extend much farther to the right of the median than to the left. This may make it a bit harder for some Machine Learning algorithms to detect patterns. We will transform these attributes later on to have more bell-shaped distributions. For our right-skewed data (i.e., tail is on the right, also called positive skew), common transformations include square root and log (we will use the log).
4.7 Data splitting
Before we get started with our in-depth data exploration, let’s split our single dataset into two: a training set and a testing set. The training data will be used to fit models, and the testing set will be used to measure model performance. We perform data exploration only on the training data.
A training dataset is a dataset of examples used during the learning process and is used to fit the models. A test dataset is a dataset that is independent of the training dataset and is used to evaluate the performance of the final model. If a model fit to the training dataset also fits the test dataset well, minimal overfitting has taken place. A better fitting of the training dataset as opposed to the test dataset usually points to overfitting.
In our data split, we want to ensure that the training and test set is representative of the various categories of median house values in the whole dataset. Take a look at 4.3
housing_df %>%
ggplot(aes(median_house_value)) +
geom_histogram(bins = 4) 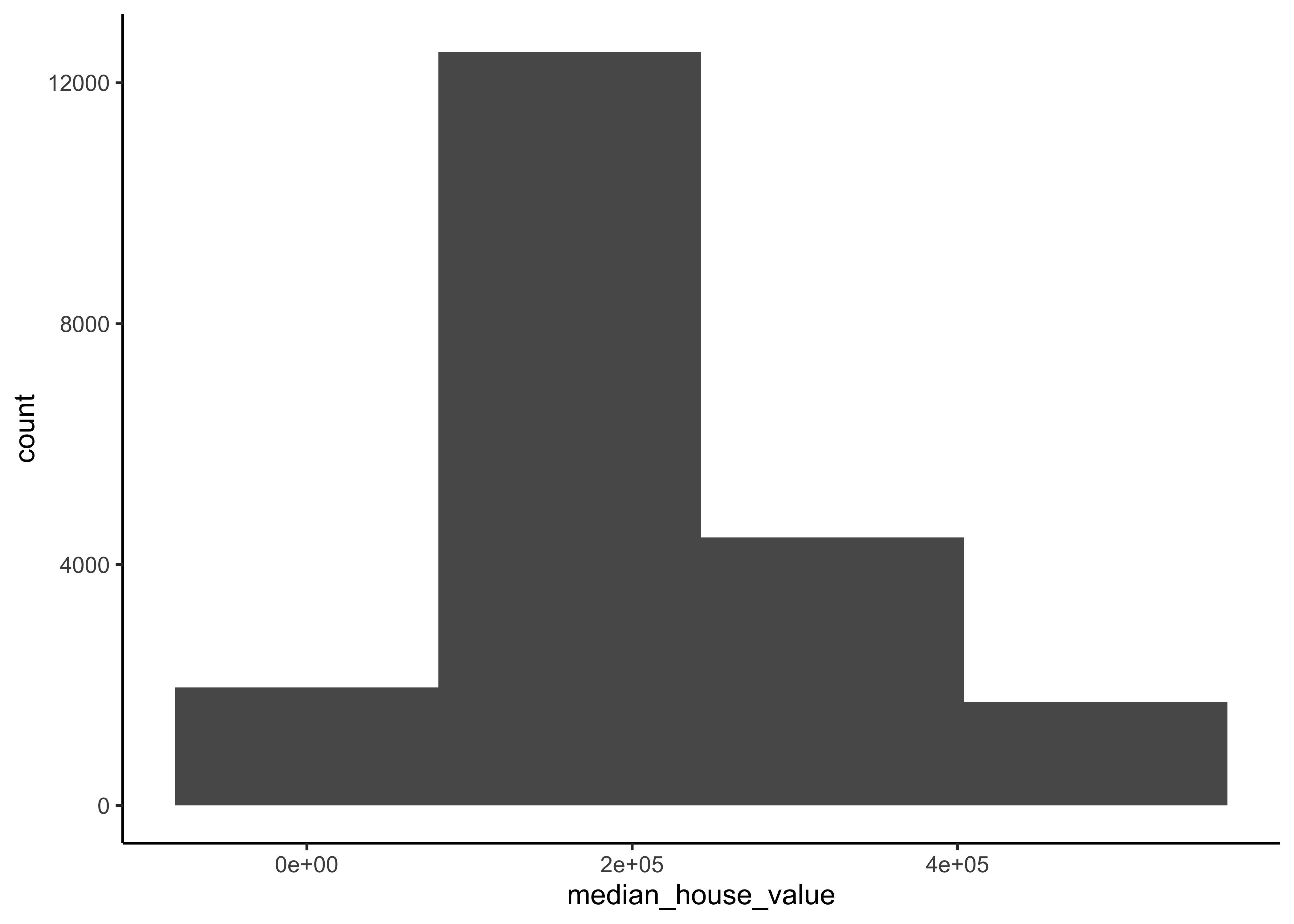
Figure 4.3: Histogram of Median Proces
In general, we would like to have instances for each stratum, or else the estimate of a stratum’s importance may be biased. A stratum (plural strata) refers to a subset (part) of the whole data from which is being sampled. You should not have too many strata, and each stratum should be large enough. We use 4 strata in our example.
To actually split the data, we can use the rsample package (included in tidymodels) to create an object that contains the information on how to split the data (which we call data_split), and then two more rsample functions to create data frames for the training and testing sets:
# Fix the random numbers by setting the seed
# This enables the analysis to be reproducible
set.seed(123)
# Put 3/4 of the data into the training set
data_split <- initial_split(housing_df,
prop = 3/4,
strata = median_house_value,
breaks = 4)
# Create dataframes for the two sets:
train_data <- training(data_split)
test_data <- testing(data_split)4.8 Data exploration
The point of data exploration is to gain insights that will help you select important variables for your model and to get ideas for feature engineering in the data preparation phase. Ususally, data exploration is an iterative process: once you get a prototype model up and running, you can analyze its output to gain more insights and come back to this exploration step. It is important to note that we perform data exploration only with our training data.
4.8.1 Create data copy
We first make a copy of the training data since we don’t want to alter our data during data exploration.
data_explore <- train_dataNext, we take a closer look at the relationships between our variables. In particular, we are interested in the relationships between our dependent variable median_house_value and all other variables. The goal is to identify possible predictor variables which we could use in our models to predict the median_house_value.
4.8.2 Geographical overview
Since our data includes information about longitude and latitude, we start our data exploration with the creation of a geographical scatterplot of the data to get some first insights:
data_explore %>%
ggplot(aes(x = longitude, y = latitude)) +
geom_point(color = "cornflowerblue")
Figure 4.4: Scatterplot of longitude and latitude
A better visualization that highlights high-density areas (with parameter alpha = 0.1 ):
data_explore %>%
ggplot(aes(x = longitude, y = latitude)) +
geom_point(color = "cornflowerblue", alpha = 0.1) 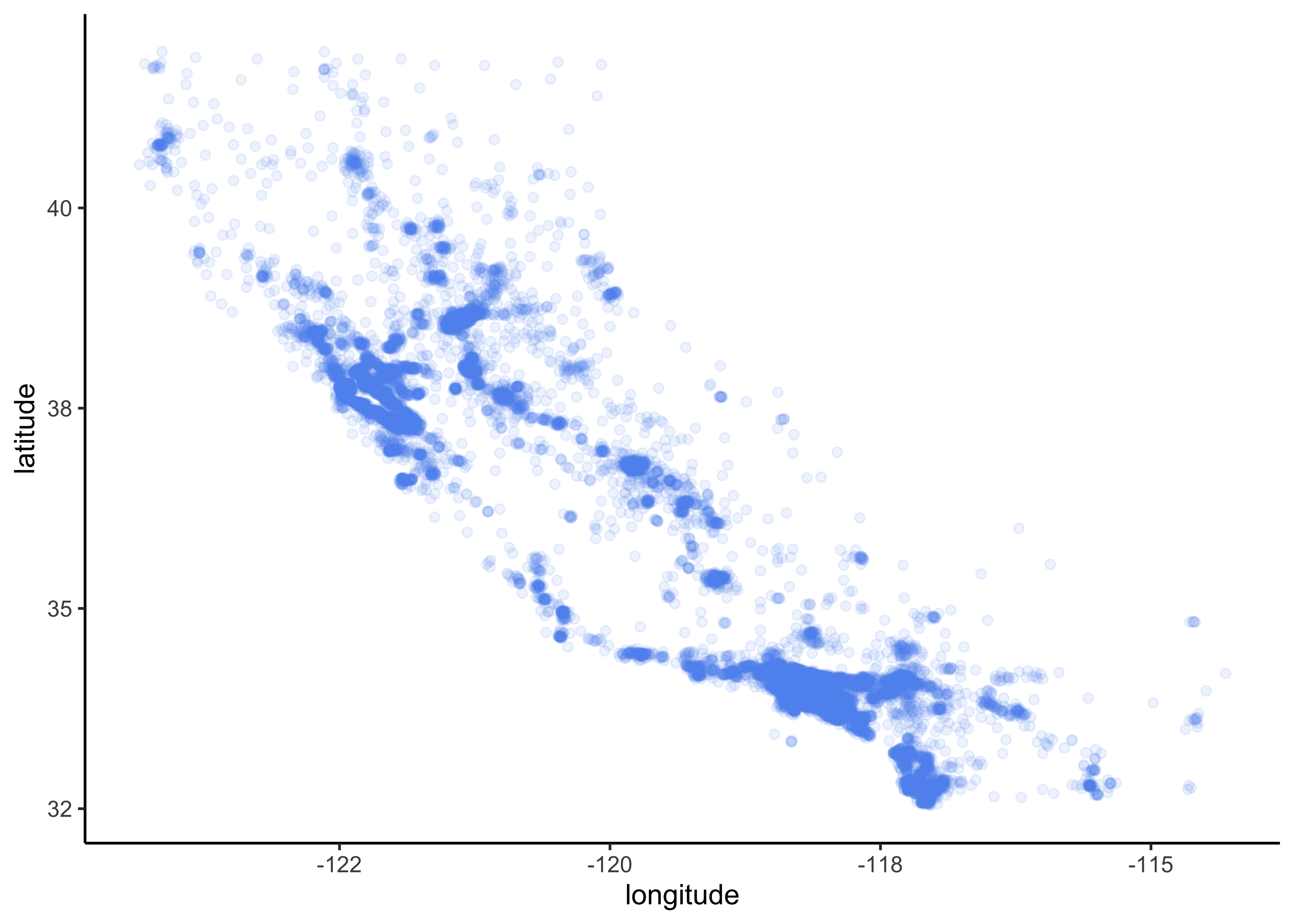
Figure 4.5: Scatterplot of longitude and latitude that highlights high-density areas
Overview about California housing prices:
- red is expensive,
- purple is cheap and
- larger circles indicate areas with a larger population.
data_explore %>%
ggplot(aes(x = longitude, y = latitude)) +
geom_point(aes(size = population, color = median_house_value),
alpha = 0.4) +
scale_colour_gradientn(colours=rev(rainbow(4)))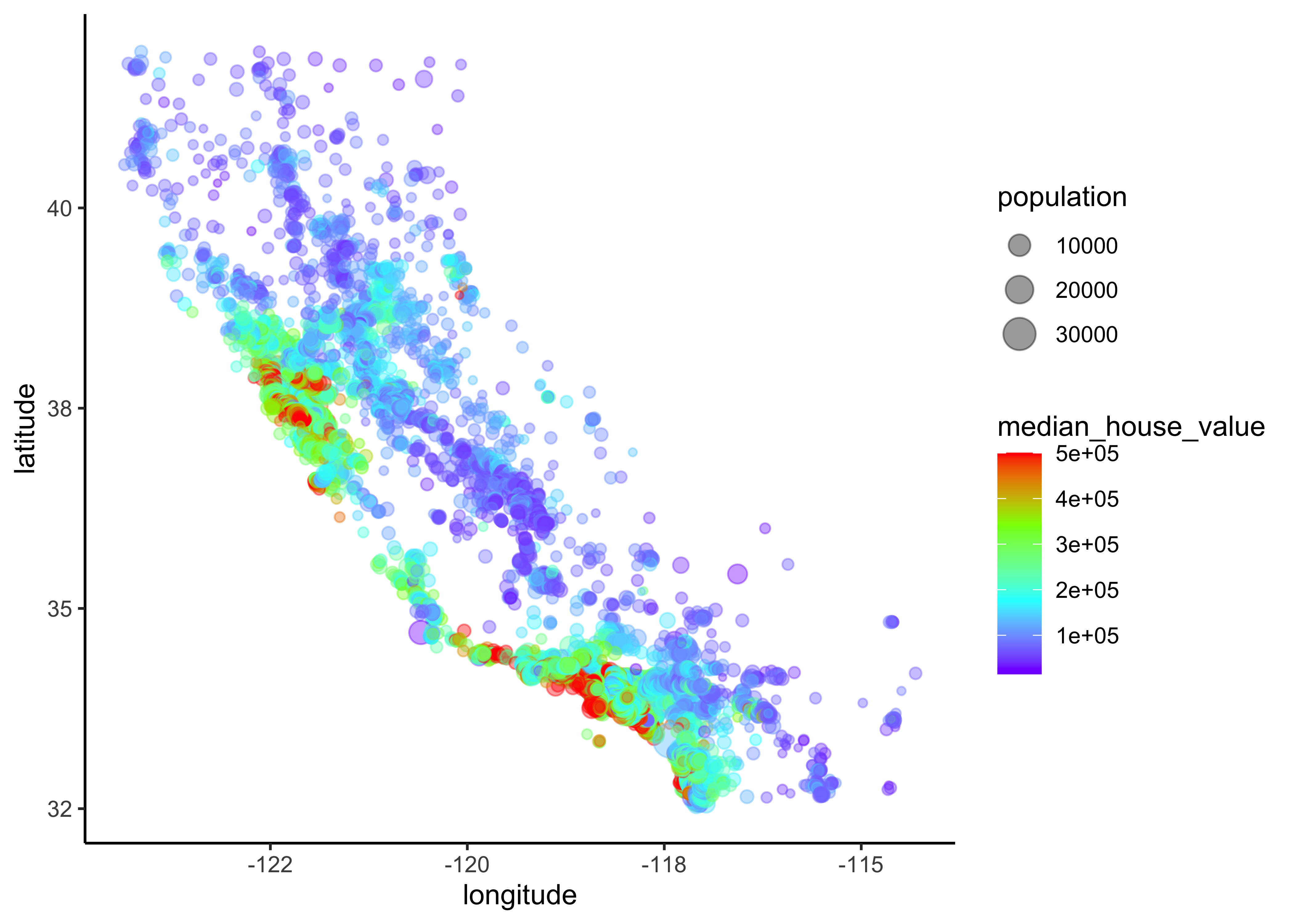
Figure 4.6: California housing_df prices
Lastly, we add a map to our data:
library(ggmap)
qmplot(x = longitude,
y = latitude,
data = data_explore,
geom = "point",
color = median_house_value,
size = population,
alpha = 0.4) +
scale_colour_gradientn(colours=rev(rainbow(4))) +
scale_alpha(guide = 'none') # don't show legend for alpha
This image tells you that the housing prices are very much related to the location (e.g., close to the ocean) and to the population density. Hence our ocean_proximity variable may be a useful predictor of median housing prices, although in Northern California the housing prices in coastal districts are not too high, so it is not a simple rule.
4.8.3 Boxplots
We can use boxplots to check, if we actually find differences in the median house value for the different levels of the categorical variable ocean_proximity. Additionally, we use the package ggsignif to calculate the significance of the difference between two of our groups and add the annotation to the plot in a single line.
library(ggsignif)
data_explore %>%
ggplot(aes(ocean_proximity, median_house_value)) +
geom_boxplot(fill="steelblue") +
xlab("Ocean proximity") +
ylab("Median house value") +
geom_signif(comparisons = list(c("<1H OCEAN", "INLAND")), # calculate significance
map_signif_level=TRUE) 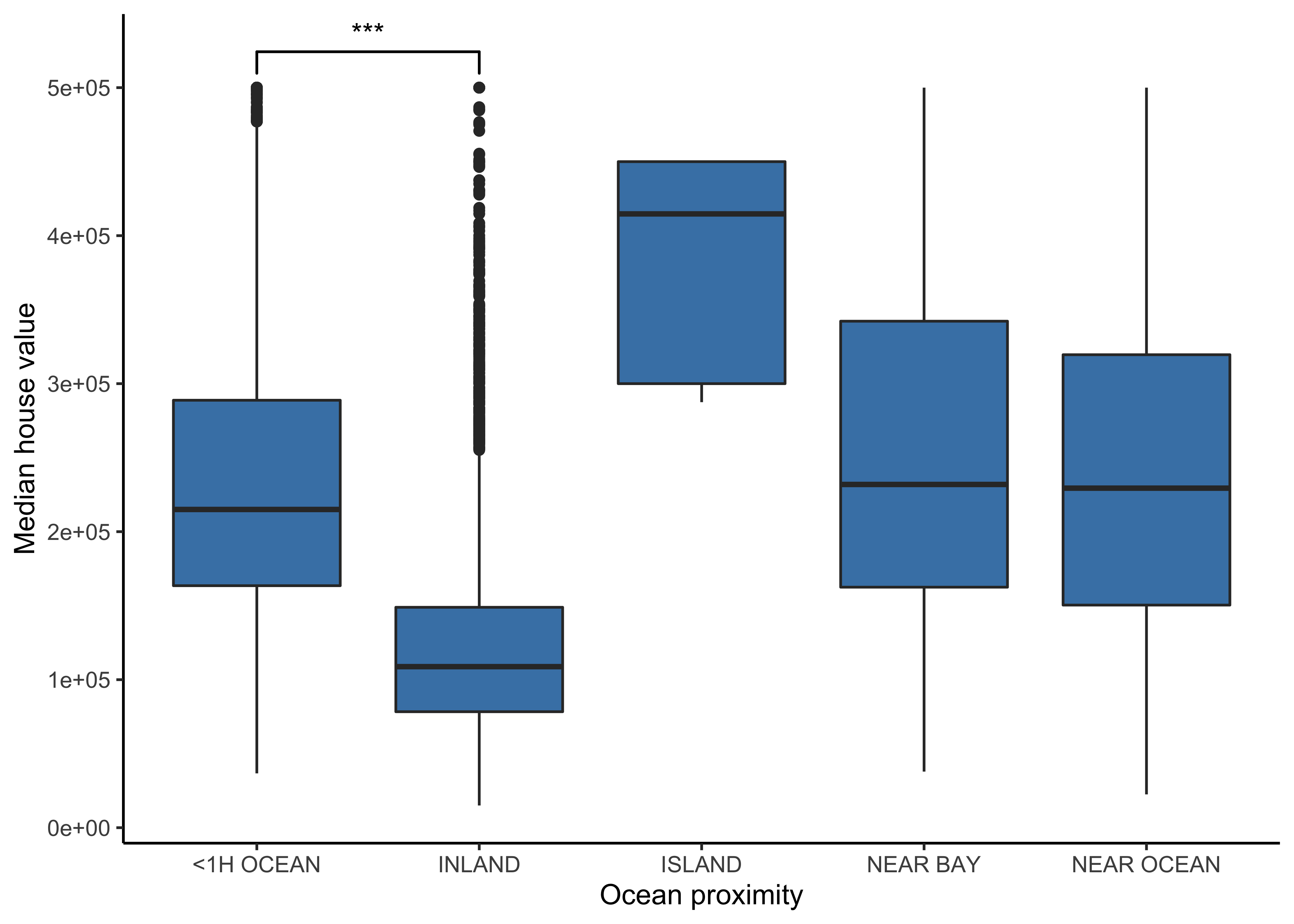
We can observe a difference in the median house value for the different levels of our categorical variable (except between “NEAR BAY” and “NEAR OCEAN”) why we should include this variable in our model. Furthermore, the difference between “<1H OCEAN” and “INLAND” is statistically significant.
4.8.4 Correlations
Now let’s analyze our numerical variables: To obtain the correlations of our numerical data, we can use the function vis_cor from the visdat package. We use Spearman’s correlation coefficient since this measure is more insensitive to outliers than Pearson’s correlation coefficient:
library(visdat)
data_explore %>%
select(where(is.numeric)) %>% # only select numerical data
vis_cor(cor_method = "spearman", na_action = "pairwise.complete.obs")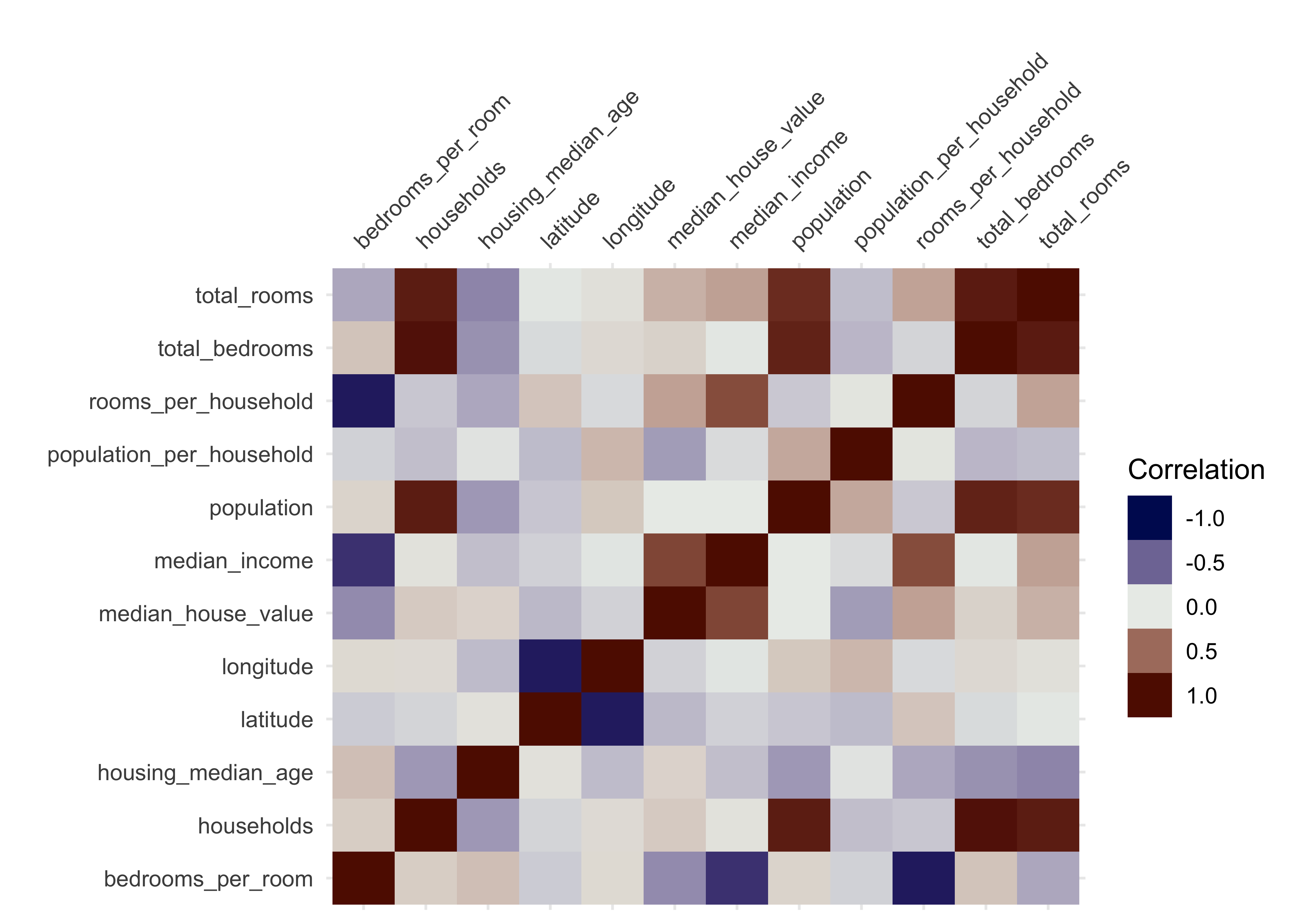
Now we take a closer look at the correlation coefficients with the package corrr.
library(corrr)
# calculate all correlations
cor_res <-
data_explore %>%
select(where(is.numeric)) %>%
correlate(method = "spearman", use = "pairwise.complete.obs")
# show correlations
cor_res %>%
select(term, median_house_value) %>%
filter(!is.na(median_house_value)) %>% # focus on dependent variable
arrange(median_house_value) %>% # sort values
fashion() # print tidy correlations#> term median_house_value
#> 1 bedrooms_per_room -.33
#> 2 population_per_household -.26
#> 3 latitude -.16
#> 4 longitude -.07
#> 5 population -.00
#> 6 housing_median_age .08
#> 7 total_bedrooms .08
#> 8 households .11
#> 9 total_rooms .20
#> 10 rooms_per_household .27
#> 11 median_income .68Furthermore, the function network_plot outputs a nice network plot of our data in which
- variables that are more highly correlated appear closer together and are joined by stronger paths.
- Paths are also colored by their sign (blue for positive and red for negative).
- The proximity of the points are determined using clustering
data_explore %>%
select(where(is.numeric)) %>%
correlate() %>%
network_plot(min_cor = .15)
Summary of our findings for the correlation analysis:
median_incomehas a strong positive correlation withmedian_house_value.the new
bedrooms_per_roomattribute is negatively correlated with themedian_house_value. Apparently houses with a lower bedroom/room ratio tend to be more expensive.rooms_per_householdis also a bit more informative than the total number of rooms (total_rooms) in a district. Obviously the larger the houses, the more expensive they are (positive correlation).population_per_householdis negatively correlated with our dependent variable.
As a last step in our correlation analysis, we check the statistical significance of Spearman’s rank correlations. In our example, we only obtain significant p-values:
cor.test(data_explore$median_house_value,
data_explore$population_per_household,
method = "spearman",
exact=FALSE)$p.value#> [1] 1.7e-245cor.test(data_explore$median_house_value,
data_explore$bedrooms_per_room,
method = "spearman",
exact=FALSE)$p.value#> [1] 0cor.test(data_explore$median_house_value,
data_explore$rooms_per_household,
method = "spearman",
exact=FALSE)$p.value#> [1] 1.6e-247cor.test(data_explore$median_house_value,
data_explore$population_per_household,
method = "spearman",
exact=FALSE)$p.value#> [1] 1.7e-245Consequently we will use this four numerical variables as well as ocean_proximity as predictors in our model.
4.8.5 Visual inspections
Now let’s analyze the choosen variables in more detail. The function ggscatmat from the package GGally creates a matrix with scatterplots, densities and correlations for numeric columns. In our code we choose an alpha level of 0.2 (for transparency).
data_explore %>%
select(median_house_value, ocean_proximity,
median_income, bedrooms_per_room, rooms_per_household,
population_per_household) %>%
ggscatmat(corMethod = "spearman",
alpha=0.2)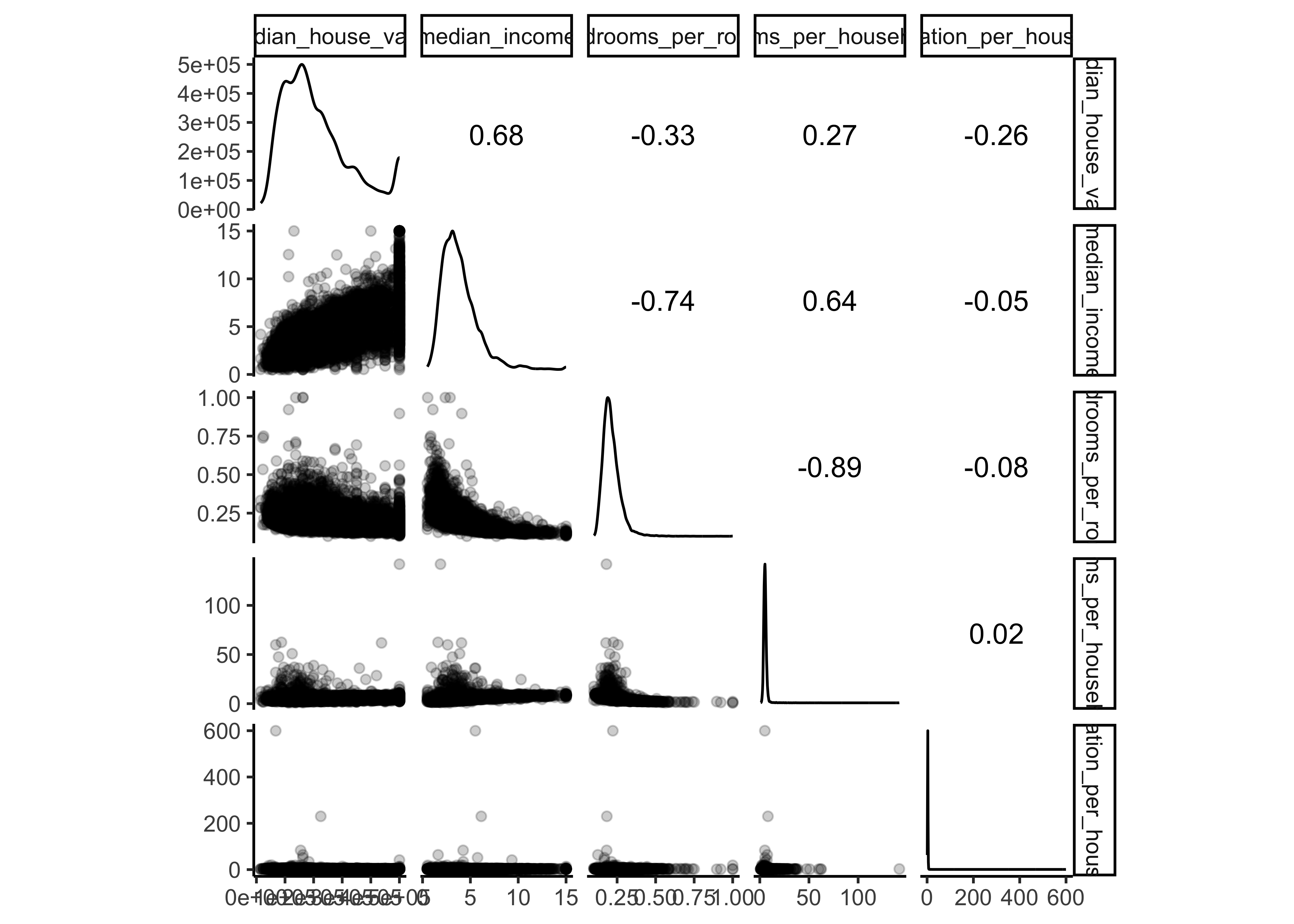
We can also add a color column for our categorical variable ocean_proximity to get even more insights about the :
data_explore %>%
select(median_house_value, ocean_proximity,
median_income, bedrooms_per_room, rooms_per_household,
population_per_household) %>%
ggscatmat(color="ocean_proximity", # add a categorical variable
corMethod = "spearman",
alpha=0.2)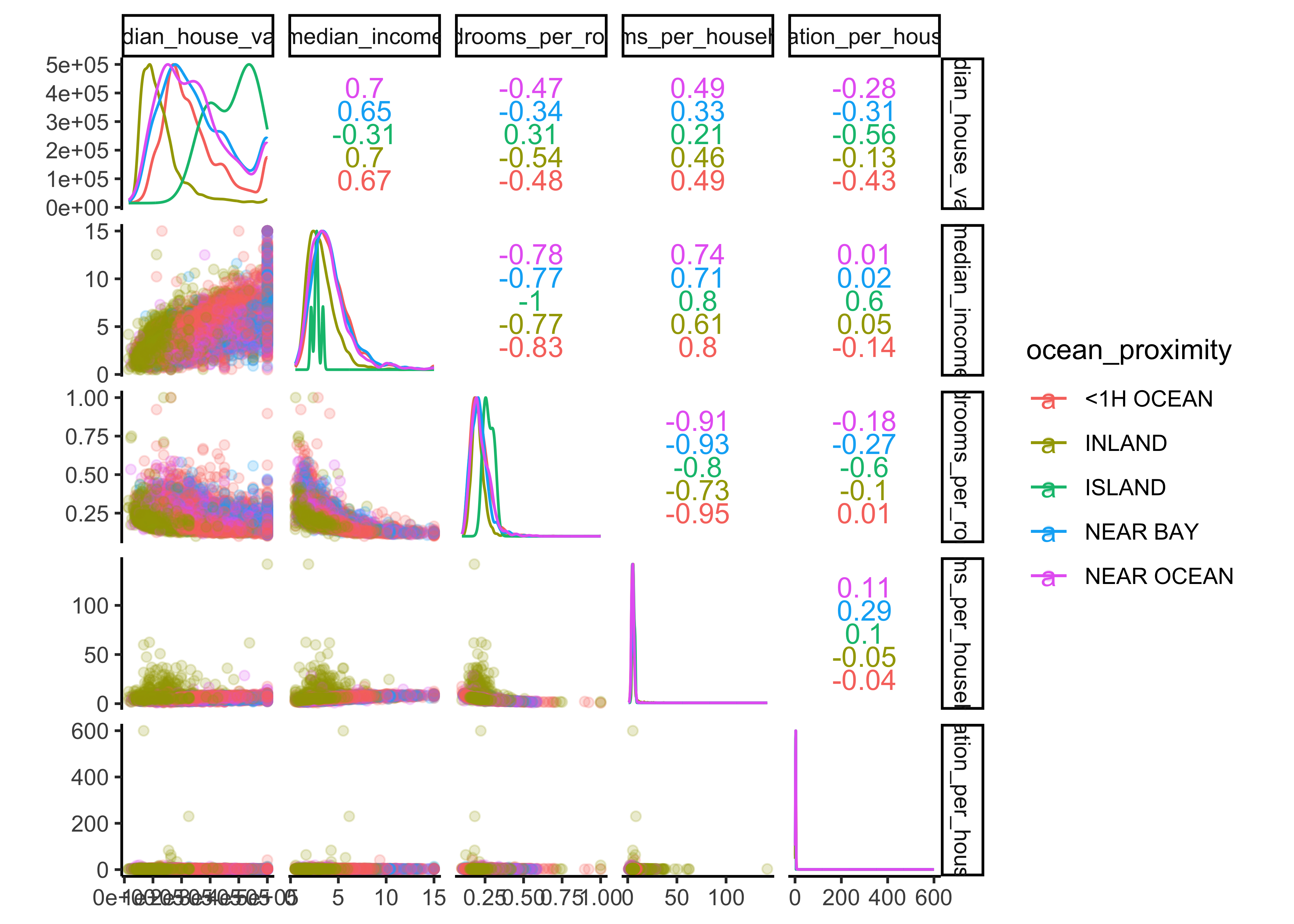
We can observe that our ocean proximity variable is indeed a good predictor for our different median house values. Another promising attribute to predict the median house value is the median income, so let’s zoom in:
data_explore %>%
ggplot(aes(median_income, median_house_value)) +
geom_jitter(color = "steelblue", alpha = 0.2) +
xlab("Median income") +
ylab("Median house value") +
scale_y_continuous(labels = scales::dollar)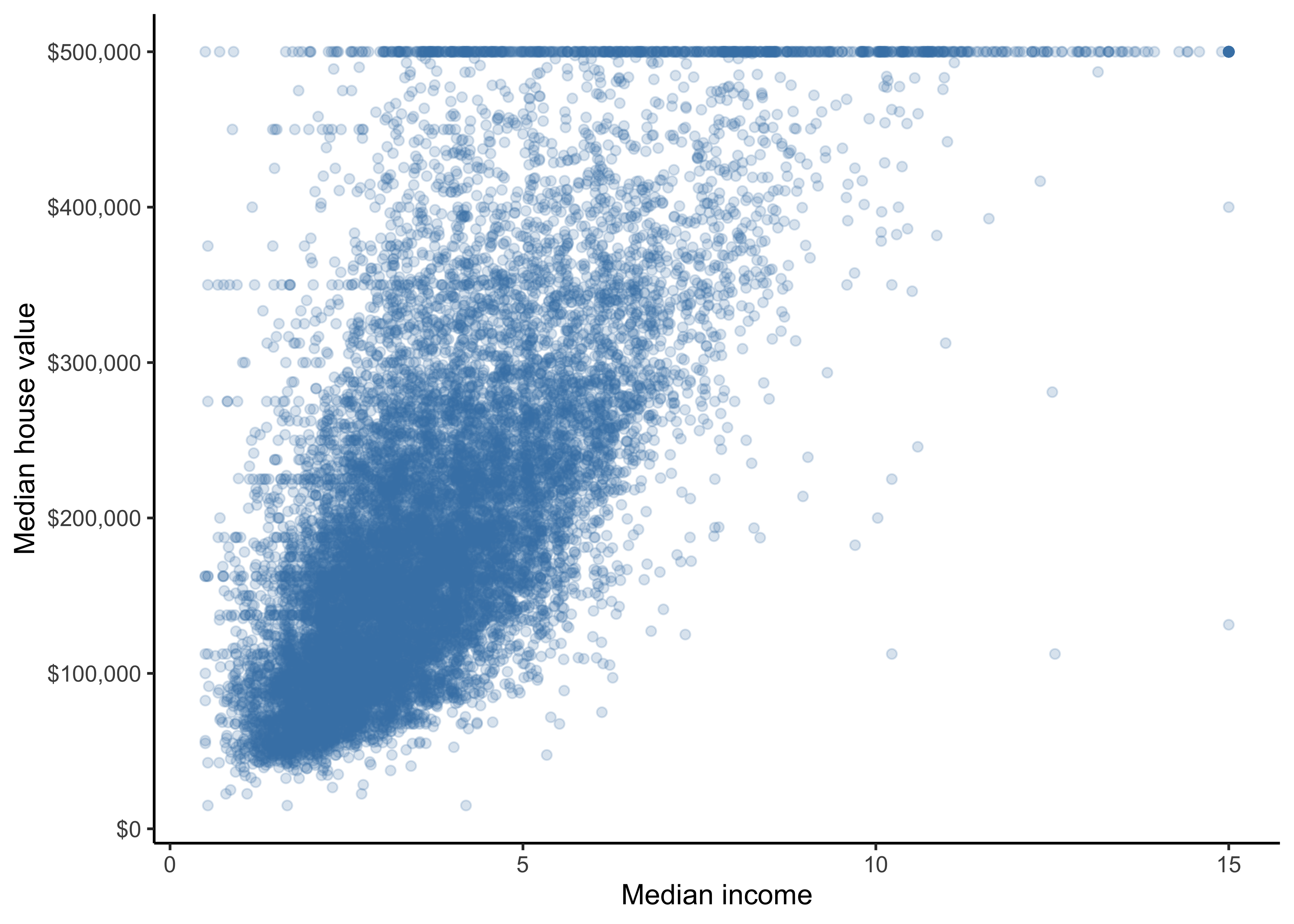
This plot reveals a few things. First, the correlation is indeed very strong; you can clearly see the upward trend, and the points are not too dispersed. Second, the price cap that we noticed earlier is clearly visible as a horizontal line at 500,000 dollars. But this plot reveals other less obvious straight lines: a horizontal line around 450,000 dollars, another around 350,000 dollars, perhaps one around $280,000 dollars, and a few more below that. Hence, in our data preparation phase we will remove districts with 500,000 dollars to prevent our algorithms from learning to reproduce these data quirks.